Conic Sections Projects using Desmos 2019 for Algebra 2 Honors or Pre-Calculus

This is only the second year that I have done Conics Projects on Desmos. (Click here for previous Conics Desmos Project post). This year, I taught conic sections in the first semester, and so I assigned this before Thanksgiving break in case students wanted to work on it. They did a fantastic job!

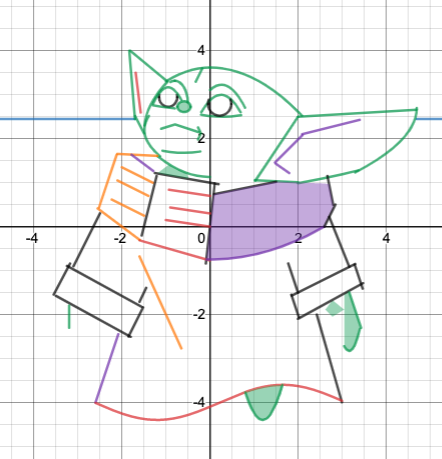
I think this project is great for several reasons, but mainly:

• It's open-ended
• They really learn about domain restrictions and intersections
• They can use conic sections as well as parent functions, so it ties concepts together
• They can relate math to something they enjoy
• It's creative
• They researched things I haven't taught them yet: inequalities, trig graphs, and lemniscates, for example

This year I added a peer review. I got the idea from my graduate class in Applied Learning. Each student was assigned a peer, and they had to say something that they liked about the project and something that they thought could be improved. They had to send this to me, and then I sent it to the peer, which ensured good quality and no negative comments. Then, the students had to make a change based on their peer's recommendation. Honestly, they gave better critical feedback than I ever could have! (See below for more info on the peer review).

Here are some of their projects.

Examples of how the Final Project was turned in:

Peer Review:

How I set up the peer review. Each student sent their project to the person after the arrow. The person after the arrow then sent their response to me, which I read and then forwarded to the student. 

 Cristi ->Will -> James->Manci-> He ->Lucas ->Bobby  ->Grace  ->Irina-> Leo->dylan  ->zach ->andres ->anthony -> niamh ->ella ->ashley ->zhongxuan ->

blake ->jack ->cristi

A Great Peer Review

Here is my Rubric.

RUBRIC 30 POINTS TOTAL

_____ 4 points Creativity

_____ 3 points Colorful

_____ 5 points Sophistication of conics

_____ 4 points Use of domain restrictions

_____ 5 points Final project with all conics shown prominently is printed in color do not wait till the last minute to do this, nor have poor printer quality and pasted on construction paper

_____ 4 points Equations printed out and pasted next to picture on construction paper (can go off the

            page if necessary.)

______5 peer review turned in on time (-2 if late per day) (graded separately – not part of 30 points)

______5 peer review emailed to me (graded separately - not part of 30 points)

______5 corrections based on peer review

How this project related to my Doctoral study in the Applied Learning Sciences

(Excerpt from my paper)

I believe that the way I teach is an amalgamation of several learning theories: Piaget’s constructivism, Papert’s constructionism, Vygotsky’s social constructivism, and even Behaviorialist theory, when I need to get facts across quickly. However, with my learning project, I am going to focus on Papert’s Constructionism, where “learners make knowledge their own,” (Kafai, 2006 p. 39) and physical objects are important. Using ideas gleaned from Piaget when he worked with him in Geneva, Seymour Papert found it was possible to learn abstract concepts concretely through objects-to-think-with. The objects my students will think with are graphs of conic sections. As of this writing, my students are learning how to graph and find equations of conics, yet I believe that they do not quite have ownership of the concept. It is something they know they need to study to pass the course, but I think that the topic is abstract and separate from them. Through the creative drawing activity, students will be transforming the ideas taught in the classroom and will express them through the website Desmos.com. Similar to LOGO, students will create designs of their choosing by “telling” the computer what to do; in this case, entering equations and playing with them until they are in the “correct spot,” that is, getting it out of their heads and onto paper. Every student can (and is encouraged to) relate conics to something that they enjoy, for example: create a beach scene, a zoo, a hockey arena, or a videogame scene, for example. The hope is that they will appropriate their knowledge to make it their own (Kafia, 2006).

Kafai, Y. B. (2006). Constructionism. In R. K. Sawyer (Ed.), The Cambridge handbook of the learning sciences (1st ed.) (pp. 35–46). Cambridge, England: Cambridge University Press.

Math Poetry Project!

My school has a Literary Magazine that gets published once a year. They ask for submissions from all students, and this year, I decided to offer an optional 20 point project where students had to write a poem about math. It was very open-ended, but it had to be worthy, in my mind, of submission. In other words, no, a Haiku did not count (yes, that was asked!) The only requirement was that students had to get a writing conference beforehand (and submit rough drafts to me, where I helped them as well.)

The results were fantastic! I strongly suggest this project because it gives students a way to discuss math and reflect on math that they so rarely get to do. So many were about anxiety. I hope writing about it made them feel better! Some are also written by students for whom English is a second language, which definitely was out of their comfort zone. I am really proud of all of my students who submitted a poem. Here are some of them, my favorite being the first one on Fixed vs. Growth mindset.
 

Test Day

Today is the day of the big math test 

Last night I studied so much I got no rest 

As the day continues I know what’s coming 

I get all nervous and my brain starts humming 

I used to arrive and take out my pencils 

But now I unpack all the utensils 

Add calculators and compasses to the list

Once the bell rings, I clench the pencil in my fist 

As the teacher begins the short review 

I start to feel like I might have the flu

I try to listen and pay attention

But I simply can’t with all this tension 

I need every fraction of a second I can get 

And as the time runs down I begin to sweat

I look up at the clock, watching the hands tick 

And stare at my paper. Which answer to pick?

As I see everyone starting to finish 

My hope of scoring well is beginning to diminish 

I must finish this page quick 

With all this stress, I might get sick

Just as I’m about to turn it in 

My entire head begins to spin 

I check through the test just once more 

Searching for any mistakes that would lower my score

The test is finally over now 

And the only thought in my mind is “wow”

After a few days of anxiously waiting 

It turns out I got a pretty good rating!

Infinity

Shall I compare it to a school’s day?

It is greater than all the galaxies,

A buffet of values that can’t be weighed.

Earth cannot contain its immensity

So grand, so fine, in its complexity,

When others try to count it, it’s in vain,

As abundant as the Aegean sea.

If others try to grasp it, it’s their bane;

Its eternalness will never once fade.

As many digits as there are in pi

Its size is comparable to a parade.

It is impossible to specify;

It is always a magnificency;

It stays the largest, as infinity.

He met math

With a glance

Through his lens

And loved it twice.

Once in China

In Winter with ice

Once in English

In one long always warm season

In different schools,

Low low scores,

On math tests,

Vanished his smiling face.

Every night, he studied and suffered. 

Many, many times

A barrier of languages tricked him. 

Time, and the sand flowing in the hourglass

Hid his broken heart.

Math made him hurt.

Math made him love.

He was and is hurt by the scores 

But among all subjects,

Math affects him the most

His love since he was small.

Today is the day of the big math test 

Last night I studied so much I got no rest 

As the day continues I know what’s coming 

I get all nervous and my brain starts humming 

I used to arrive and take out my pencils 

But now I take out all the utensils 

Add calculators, compasses, and graph paper to the list

Once the bell rings, I clench the pencil in my fist 

As the teacher begins the short review 

I feel like I might have the flu

I try to listen and pay attention

But I simply can’t with all this tension 

I need every fraction of a second I can get 

And as the time runs down I begin to sweat

I look up at the clock, watching the hands tick 

And stare at my paper. Which answer to pick?

As I see everyone starting to finish 

My hope of scoring well is beginning to diminish 

I must finish this page quick 

With all this stress, I might get sick

Just as I’m about to turn it in 

My entire head begins to spin 

I check through it once more 

Searching for any mistakes that would lower my score

The test is finally over now 

And the only thought in my mind is “wow”

After a few days of anxiously waiting 

It turns out I got a pretty good rating.

In eighth grade, I was so good at math,

Now that thought just makes me laugh.

Nine more hours till the test,

Just keep studying and hope for the best.

Slope, range, and domain

All floating through my brain.

Seven more hours I have to study

To try to make Algebra II my buddy.

So many formulas in my head,

Don’t think I will ever get to bed.

Five more hours till the test,

Now is not the time to rest.

The long word problems cause me pain,

There’s my grade down the drain.

Three more hours to gain knowledge,

With a C in math, will I get into college?

As graphs of equations circle my brain

I wonder, will conics drive me insane?

One more hour until I’m done.

Maybe studying functions will be more fun.

In-Test Stress

Equations flowing through my veins

Transformations filling up my brains

Numbers racing through my head

“You don’t need to study more!” is what my mom said

Little did I know that she was very incorrect

It seems that this test has surpassed my natural intellect

As I search my memory for previous knowledge

I question if I will ever be accepted into my dream college

I know, I know, I’m being melodramatic

But how in the world does one graph a quadratic?

Parabolas, hyperbolas, curves, and more

It’s looking like I won’t get a good score

But then it comes to me, parent functions and all!

Maybe this test won’t be my downfall

My pencil starts to write very fast

I begin to put my confusion into the past

Domain and range? Easy, I know this

There is not one question that I will miss!

Seven minutes remaining on the clock

I’m reviewing my answers, my focus in lock

Two minutes to go and I turn in my test.

A huge weight has been lifted off my chest.

Next time, I will make sure not to get so upset

Because if I try my best, it’s a deserving grade I will get.

Life is Mathematic

Life can be like a linear function

But when challenges arise, it’s like the sine

Challenges can give life vibration

While without them life is a straight line

Life can be like a linear function

While troubles can be like holes

Holes may halt the function

But the function always continues

Life can be like a linear function

And your attitude can be the slope

A positive attitude gives life ascension

While a negative attitude can only cause a drop

Life can be like a linear function

And I hope you perceive your life with satisfaction

Functions are like karma, 

you give something you get something.

Functions are unique,

different parent functions and different graphs.

Functions must pass a test, 

a vertical line on a graph to prove one input goes to exactly one output.

Functions can be treated like numbers, 

you can subtract, multiply, divide, and add them together.

Functions can be like mountains,

intervals of increases and decreases, and peaks and troughs.

Functions are like long movies,

sometimes they just never seem to end.

Functions are also like toddlers,

they can’t always go very far before stopping.

Functions are like elevators, 

they go up and down but not always forever.

Functions can be expressed in many forms, 

equations, graphs, maps, or tables.

Functions are like rollercoasters,

up and down, and steep and not.

Functions are patterns, 

easy to predict and always following a rule.

Functions are like a crystal ball,

they help us to predict the future.

Functions are like glasses, 

they enable us to see and visualize real-world things.

Functions are like blueprints,

they enable us to easily understand how the world works the way it does.

It winds you through its paths

Gives you calculations on top of calculations

All in pursuit of the satisfying solution

But, make one mistake

And that answer is gone

So very treacherous

These twists and turns

Of mathematics can be

Equations on top of equations

Operations, for example

Can put you on a rollercoaster of math  

Like the graph of sine

And then, after so much calculation

The work results in one painfully simple solution

Like one

(5xy + 6x^7+9y^18)^0

If one does not notice

In a brief moment of not paying attention

That there is an exponent 0

They might puzzle themselves with the problem for hours

Mathematics

The solving of every problem is a journey

Filled with highs and lows 

Like the maxes and mins of a parabola

At some points, the min is hit

One might consider giving up 

But when they decide to continue

And then finally scramble through the last calculations

And box in the set of numbers that answers their questions

How satisfyingly simple it is

What a numerical miracle

What a feeling of giddiness fills the person at that very moment

Because of mathematics

Mathematics, which is really just

One long, arduous journey 

Made up brick by brick 

Problem by problem

Number by number

focusing, scribbling, erasing, and rewriting

these are parts of the thrill of math.

graphing, translating, reflecting, and shifting 

even if it involves making mistakes

when you’re passionate about something

just doing it sparks joy

sitting, plotting, computing, and 

graphing, translating, reflecting, and shifting

can bring such satisfaction.

formulating, equating, expressing, and understanding,

it requires hard work,

time

dedication

and passion

but in the end, it is worth it.

working, thinking, calculating, and stretching your brain

when the difficulty rises,

there are challenging problems,

that are not so easy.

but a part of the joy of solving

is doing these things

in ways you might not have thThe Missing Variable: x2 + 9x + 20 = 0 

Something is missing

An incomplete whole

For x I can’t find

Its answer, my goal

The problem seems hard

We do not comprehend

Try and we try

But we hit a dead-end

We cannot give up

Commitment is key

We must solve for x

Then we’ll be free

Digits on the right

Then zero we said

Quadratic formula?

Factoring instead

Put parenthesis

X has been squared

For two solutions

Do not be scared

Nine’s the coefficient

But it’s not lonely

There is a constant

Of twenty only

Multiplies as twenty

Adds to be just nine

I will guess and check

Till these numbers fit fine

Could it be two and ten?

When added, twelve is seen

What about six and three?

Multiplied it’s eighteen

Factoring is hard

Too many numbers

Forever my mind

Will be full of wonders

Wait! I got it?

The answer is mine

Added it’s twenty 

Together it’s nine

After many efforts

Four and five will work

The problem’s nearly done

Soon I can smirk

X plus five is zero

also works with four

Just two solutions

There are not any more

Now subtract the numbers

Onto the other side

Negative four, negative five

I am filled with pride

X was hard to find

There was a struggle

With math you must grind

But after the trouble

There has been a breakthrough

Something is clear

You have reached success

The end, you are here

Night-gebra

By my nightlight, I study my book

I’ll learn these equations

By hook or by crook

Hours are spent finding eccentricities

Staring at these complex ellipticities

I scramble to simplify

As I kiss my sleep goodbye

I put in my airpods

Thinking about the odds

The rhythm makes me tap

Feeling it’s a trap

Wishing I could figure it out 

But all I do is doubt

My abilities?

All liabilities!

The crescent moon shines into my window

Oh how I wish to lay on my pillow

But the problems go round and round with no near end

As I search every corner for a dividend

My morning alarm starts to blare

Algebra hates me, I swear

Should I give up and just stay at home?

It’s easier to write a poem!

Sir Cull

360 degrees 

and a shape that always puts you at ease,

I come in all different sizes, always aiming to please.

I am defined by area, which can vary,

But fear not, my radius and pi are not very scary.

There is also an equation for my shape, which has many components

If you know these are the center and radius, then you are in the bonus!

The points defined as the center are k and h,

But be careful because in the equation, they are not so great!
They are not so great because they are opposites of their true value

Which trips people up and makes them blue.

H is subtracted from X while Y subtracts K,

Don’t forget to put each in parentheses and square, or Mrs. Winer will not let you stay!

Do not get excited as there are a couple more steps,

But do not be scared because these are easier than the rest!

Add an addition sign between the two terms, which will almost wrap it up,

Then do not forget to add an equal sign, and the last term is abrupt!
The most important part as we see it in every circle equation,

It is the radius, and will never go under the process of evasion!

Don’t forget to square the radius at the end though,

Because if you do not, the problem will not flow!

Last but not least, there is another term that you can not forget,

It is defined by 2𝛑r, so don’t you fret!

It defines the perimeter of the circle, which is essential,

But do not overhype the circumference, as it is not always frequential.

As you can see, circles like me are fun,

Just because they are complicated does not mean they cannot be a pun.

After all, everyone is complicated and that is a fact,

Without complications no one would be in tact.

And most importantly, without problems, there would not be math,

And without math, the idea of me, as a circle, would never be in your path!

Maybe you guessed, maybe you could not

But I am the greatest, being the only alive shape that you got.

I am the one,

The only,

Mr. Sir Cull

Clarity in the Storm

Swirls of numbers,

No order to be found

They run rapidly through my mind

The pieces don’t fit,

I see no respite from the chaos

Then slowly the storm starts to calm,

With time I see clearly,

I’m no longer overwhelmed

Every breath calms me 

The world stops spinning 

Deep breath,

Step one,

Deep breath,

Step two,

The clouds are fading away 

Finally, I’ve opened a gap in the clouds

Patterns,

Everywhere, they repeat  

They guide me forwards

Clarity like never before

Before, the storm swept me up,

But now, I’m carried high above the chaos below

Winds swirl like cube root functions

I’m lifted through inequalities and decimals

I feel a weight lifted from my shoulders

The equations start to fit,

Pieces connect in new ways,,

The chaos of the storm is gone

What I need is right here,

I’ve made sense of what’s in front of me

Something shimmers in the distance

The concept floats closer and closer

Through the mist I see it faintly, 

Warm rays meet me with satisfaction

The answer to my confusion is here

Today has been a long day

I have had so much to do

I can’t even find the right words to say 

But I have to see the day through.

I may have drifted off in class

I probably should have paid more attention

But I didn’t realize we were going so fast 

And I know you have the best intention

I started to focus again 

And looked at the board

But all I saw were marks of pen

And my brain just spiraled downward

So I find it a bit of a challenge

To be the best, to know the most

When the lack of sleep has done so much damage

All day during school I feel like a ghost. 

I can’t seem to grasp the concepts like everyone else

I take a bit more time

But when I do, the feeling is like nothing else 

And the world feels like it’s mine

There come the days I want to give up

Because I get the problem wrong every time

My world is not going to blow up 

So I need to finish the climb

I wake up I study 

I study all day

I always feel so cruddy

And I never have time to play 

But when I get the problem right

I feel like I can touch the sky

My face lights up so bright

And you can see teardrops in my eye